Само понятие иррационального числа так устроено, что оно определяется через отрицание свойства "быть рациональным", поэтому доказательство от противного является здесь наиболее естественным. Можно, однако предложить вот какое рассуждение.
Чем отличаются принципиально рациональные числа от иррациональных? Как те, так и другие, можно приблизить рациональными числами с любой заданной точностью, но для рациональных чисел имеется приближение с "нулевой" точностью (самим этим числом), а для иррациональных чисел это уже не так. Попытаемся на этом "сыграть".
Прежде всего, отметим такой простой факт. Пусть $%\alpha$%, $%\beta$% -- два положительных числа, которые приближают друг друга с точностью $%\varepsilon$%, то есть $%|\alpha-\beta|=\varepsilon$%. Что произойдёт, если мы заменим числа на обратные? Как при этом изменится точность? Легко видеть, что $$\left|\frac1\alpha-\frac1\beta\right|=\frac{|\alpha-\beta|}{\alpha\beta}=\frac{\varepsilon}{\alpha\beta},$$ что будет строго меньше $%\varepsilon$% при $%\alpha\beta>1$%. Это утверждение можно рассматривать в качестве самостоятельной леммы.
Теперь положим $%x=\sqrt{2}$%, и пусть $%q\in{\mathbb Q}$% -- рациональное приближение числа $%x$% с точностью $%\varepsilon$%. Мы знаем, что $%x>1$%, а насчёт приближения $%q$% потребуем выполнения неравенства $%q\ge1$%. У всех чисел, меньших $%1$%, точность приближения будет хуже, чем у самой $%1$%, и потому мы не будем их рассматривать.
К каждому из чисел $%x$%, $%q$% прибавим по $%1$%. Очевидно, точность приближения останется той же. Теперь у нас есть числа $%\alpha=x+1$% и $%\beta=q+1$%. Переходя к обратным числам и применяя "лемму", мы придём к выводу, что точность приближения у нас улучшилась, став строго меньше $%\varepsilon$%. Требуемое условие $%\alpha\beta>1$% у нас соблюдено даже с запасом: на самом деле мы знаем, что $%\alpha>2$% и $%\beta\ge2$%, откуда можно сделать вывод, что точность улучшается как минимум в $%4$% раза, то есть не превосходит $%\varepsilon/4$%.
И вот здесь -- основной момент: по условию, $%x^2=2$%, то есть $%x^2-1=1$%, а это значит, что $%(x+1)(x-1)=1$%, то есть числа $%x+1$% и $%x-1$% обратны друг другу. А это означает, что $%\alpha^{-1}=x-1$% будет приближением к (рациональному) числу $%\beta^{-1}=1/(q+1)$% c точностью строго меньше $%\varepsilon$%. Осталось прибавить по $%1$% к этим числам, и окажется, что у числа $%x$%, то есть у $%\sqrt{2}$%, появилось новое рациональное приближение, равное $%\beta^{-1}+1$%, то есть $%(q+2)/(q+1)$%, с "улучшенной" точностью. Это завершает доказательство, так как у рациональных чисел, как мы отмечали выше, существует "абсолютно точное" рациональное приближение с точностью $%\varepsilon=0$%, где точность в принципе повысить нельзя. А мы сумели это сделать, что говорит об иррациональности нашего числа.
Фактически, это рассуждение показывает, как строить конкретные рациональные приближения для $%\sqrt{2}$% со всё улушающейся точностью. Надо сначала взять приближение $%q=1$%, и далее применять одну и ту же формулу замены: $%q\mapsto(q+2)/(q+1)$%. В ходе этого процесса получается следующее: $$1,\frac32,\frac75,\frac{17}{12},\frac{41}{29},\frac{99}{70}$$ и так далее.
Что такое иррациональные числа? Почему они так называются? Где они используются и что собой представляют? Немногие могут без раздумий ответить на эти вопросы. Но на самом деле ответы на них довольно просты, хоть нужны не всем и в очень редких ситуациях
Сущность и обозначение
Иррациональные числа представляют собой бесконечные непериодические Необходимость введения этой концепции обусловлена тем, что для решения новых возникающих задач уже было недостаточно ранее имеющихся понятий действительных или вещественных, целых, натуральных и рациональных чисел. Например, для того, чтобы вычислить, квадратом какой величины является 2, необходимо использовать непериодические бесконечные десятичные дроби. Кроме того, многие простейшие уравнения также не имеют решения без введения концепции иррационального числа.
Это множество обозначается как I. И, как уже ясно, эти значения не могут быть представлены в виде простой дроби, в числителе которой будет целое, а в знаменателе -
Впервые так или иначе с этим явлением столкнулись индийские математики в VII веке когда было обнаружено, что квадратные корни из некоторых величин не могут быть обозначены явно. А первое доказательство существования подобных чисел приписывают пифагорейцу Гиппасу, который сделал это в процессе изучения равнобедренного прямоугольного треугольника. Серьезный вклад в изучение этого множества привнесли еще некоторые ученые, жившие до нашей эры. Введение концепции иррациональных чисел повлекло за собой пересмотр существовавшей математической системы, вот почему они так важны.
Происхождение названия
Если ratio в переводе с латыни - это "дробь", "отношение", то приставка "ир"
придает этому слову противоположное значение. Таким образом, название множества этих чисел говорит о том, что они не могут быть соотнесены с целым или дробным, имеют отдельное место. Это и вытекает из их сущности.
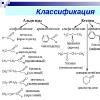
Место в общей классификации
Иррациональные числа наряду с рациональными относится к группе вещественных или действительных, которые в свою очередь относятся к комплексным. Подмножеств нет, однако различают алгебраическую и трансцендентную разновидность, о которых речь пойдет ниже.

Свойства
Поскольку иррациональные числа - это часть множества действительных, то к ним применимы все их свойства, которые изучаются в арифметике (их также называют основными алгебраическими законами).
a + b = b + a (коммутативность);
(a + b) + c = a + (b + c) (ассоциативность);
a + (-a) = 0 (существование противоположного числа);
ab = ba (переместительный закон);
(ab)c = a(bc) (дистрибутивность);
a(b+c) = ab + ac (распределительный закон);
a x 1/a = 1 (существование обратного числа);
Сравнение также проводится в соответствии с общими закономерностями и принципами:
Если a > b и b > c, то a > c (транзитивность соотношения) и. т. д.
Разумеется, все иррациональные числа могут быть преобразованы с помощью основных арифметических действий. Никаких особых правил при этом нет.

Кроме того, на иррациональные числа распространяется действие аксиомы Архимеда. Она гласит, что для любых двух величин a и b справедливо утверждение, что, взяв a в качестве слагаемого достаточное количество раз, можно превзойти b.
Использование
Несмотря на то что в обычной жизни не так уж часто приходится сталкиваться с ними, иррациональные числа не поддаются счету. Их огромное множество, но они практически незаметны. Нас повсюду окружают иррациональные числа. Примеры, знакомые всем, - это число пи, равное 3,1415926..., или e, по сути являющееся основанием натурального логарифма, 2,718281828... В алгебре, тригонометрии и геометрии использовать их приходится постоянно. Кстати, знаменитое значение "золотого сечения", то есть отношение как большей части к меньшей, так и наоборот, также

относится к этому множеству. Менее известное "серебряное" - тоже.
На числовой прямой они расположены очень плотно, так что между любыми двумя величинами, отнесенными к множеству рациональных, обязательно встречается иррациональная.
До сих пор существует масса нерешенных проблем, связанных с этим множеством. Существуют такие критерии, как мера иррациональности и нормальность числа. Математики продолжают исследовать наиболее значительные примеры на предмет принадлежности их к той или иной группе. Например, считается, что е - нормальное число, т. е. вероятность появления в его записи разных цифр одинакова. Что же касается пи, то относительно его пока ведутся исследования. Мерой иррациональности же называют величину, показывающую, насколько хорошо то или иное число может быть приближено рациональными числами.
Алгебраические и трансцендентные
Как уже было упомянуто, иррациональные числа условно разделяются на алгебраические и трансцендентные. Условно, поскольку, строго говоря, эта классификация используется для деления множества C.
Под этим обозначением скрываются комплексные числа, которые включают в себя действительные или вещественные.
Итак, алгебраическим называют такое значение, которое является корнем многочлена, не равного тождественно нулю. Например, квадратный корень из 2 будет относиться к этой категории, поскольку он является решением уравнения x 2 - 2 = 0.
Все же остальные вещественные числа, не удовлетворяющие этому условию, называются трансцендентными. К этой разновидности относятся и наиболее известные и уже упомянутые примеры - число пи и основание натурального логарифма e.

Что интересно, ни одно, ни второе не были изначально выведены математиками в этом качестве, их иррациональность и трансцендентность были доказаны через много лет после их открытия. Для пи доказательство было приведено в 1882 году и упрощено в 1894, что положило конец спорам о проблеме квадратуры круга, которые длились на протяжении 2,5 тысяч лет. Оно до сих пор до конца не изучено, так что современным математикам есть над чем работать. Кстати, первое достаточно точное вычисление этого значения провел Архимед. До него все расчеты были слишком приблизительными.
Для е (числа Эйлера или Непера), доказательство его трансцендентности было найдено в 1873 году. Оно используется в решении логарифмических уравнений.
Среди других примеров - значения синуса, косинуса и тангенса для любых алгебраических ненулевых значений.
1.Доказательство является примерами дедуктивного рассуждения и отличаются от индуктивных или эмпирических аргументов. Доказательство должно продемонстрировать, что доказываемое утверждение всегда верно, иногда путем перечисления всех возможных случаев и показывая, что утверждение выполняется в каждом из них. Доказательство может опираться на очевидные или общепринятые явления или случаи, известные как аксиомы. Вопреки этому, доказывается иррациональность “корня квадратного из двух”.
2.Вмешательство топологии здесь объясняется самой природой вещей, что означает, что чисто алгебраического способа доказательства иррациональности, в частности, исходя из рациональных чисел нет.Вот пример, за вами право выбора: 1+1/2 + 1/4 + 1/8 ….= 2 или 1+1/2 + 1/4 + 1/8 …≠ 2 ???
Если вы примете 1+1/2 + 1/4 + 1/8 +…= 2, что считается “алгебраическим” подходом, то совсем не составляет труда показать, что существует n/m ∈ ℚ, которое на бесконечной последовательности является иррациональным и конечным числом.Это подсказывает, что иррациональные числа являются замыканием поля ℚ, но это относится к топологической особенности.
Так для чисел Фибоначчи, F(k): 1,1,2,3,5,8,13,21,34,55,89,144,233,377, … lim{F(k+1)/F(k)} = φ
Это лишь показывает, что существует непрерывный гомоморфизм ℚ → I, и можно показать строго, что существования такого изоморфизма не является логическим следствием алгебраических аксиом.
Понимание чисел, особенно натуральных чисел, является одним из старейших математических "умений". Многие цивилизации, даже современные, приписывали числам некие мистические свойства ввиду их огромной важности в описании природы. Хотя современная наука и математика не подтверждают эти "волшебные" свойства, значение теории чисел неоспоримо.
Исторически сначала появилось множество натуральных чисел, затем довольно скоро к ним добавились дроби и положительные иррациональные числа. Ноль и отрицательные числа были введены после этих подмножеств множества действительных чисел. Последнее множество, множество комплексных чисел, появилось только с развитием современной науки.
В современной математике числа вводят не в историческом порядке, хотя и в довольно близком к нему.
Натуральные числа $\mathbb{N}$
Множество натуральных чисел часто обозначается как $\mathbb{N}=\lbrace 1,2,3,4... \rbrace $, и часто его дополняют нулем, обозначая $\mathbb{N}_0$.
В $\mathbb{N}$ определены операции сложения (+) и умножения ($\cdot$) со следующими свойствами для любых $a,b,c\in \mathbb{N}$:
1. $a+b\in \mathbb{N}$, $a\cdot b \in \mathbb{N}$ множество $\mathbb{N}$ замкнуто относительно операций сложения и умножения
2. $a+b=b+a$, $a\cdot b=b\cdot a$ коммутативность
3. $(a+b)+c=a+(b+c)$, $(a\cdot b)\cdot c=a\cdot (b\cdot c)$ ассоциативность
4. $a\cdot (b+c)=a\cdot b+a\cdot c$ дистрибутивность
5. $a\cdot 1=a$ является нейтральным элементом для умножения
Поскольку множество $\mathbb{N}$ содержит нейтральный элемент для умножения, но не для сложения, добавление нуля к этому множеству обеспечивает включение в него нейтрального элемента для сложения.
Кроме этих двух операций, на множестве $\mathbb{N}$ определены отношения "меньше" ($
1. $a b$ трихотомия
2. если $a\leq b$ и $b\leq a$, то $a=b$ антисимметрия
3. если $a\leq b$ и $b\leq c$, то $a\leq c$ транзитивность
4. если $a\leq b$, то $a+c\leq b+c$
5. если $a\leq b$, то $a\cdot c\leq b\cdot c$
Целые числа $\mathbb{Z}$
Примеры целых чисел:
$1, -20, -100, 30, -40, 120...$
Решение уравнения $a+x=b$, где $a$ и $b$ - известные натуральные числа, а $x$ - неизвестное натуральное число, требует введения новой операции - вычитания(-). Если существует натуральное число $x$, удовлетворяющее этому уравнению, то $x=b-a$. Однако, это конкретное уравнение не обязательно имеет решение на множестве $\mathbb{N}$, поэтому практические соображения требуют расширения множества натуральных чисел таким образом, чтобы включить решения такого уравнения. Это приводит к введению множества целых чисел: $\mathbb{Z}=\lbrace 0,1,-1,2,-2,3,-3...\rbrace$.
Поскольку $\mathbb{N}\subset \mathbb{Z}$, логично предположить, что введенные ранее операции $+$ и $\cdot$ и отношения $
1. $0+a=a+0=a$ существует нейтральный элемент для сложения
2. $a+(-a)=(-a)+a=0$ существует противоположное число $-a$ для $a$
Свойство 5.:
5. если $0\leq a$ и $0\leq b$, то $0\leq a\cdot b$
Множество $\mathbb{Z} $ замкнуто также и относительно операции вычитания, то есть $(\forall a,b\in \mathbb{Z})(a-b\in \mathbb{Z})$.
Рациональные числа $\mathbb{Q}$
Примеры рациональных чисел:
$\frac{1}{2}, \frac{4}{7}, -\frac{5}{8}, \frac{10}{20}...$
Теперь рассмотрим уравнения вида
$a\cdot x=b$, где $a$ и $b$ - известные целые числа, а $x$ - неизвестное. Чтобы решение было возможным, необходимо ввести операцию деления ($:$), и решение приобретает вид $x=b:a$, то есть $x=\frac{b}{a}$. Опять возникает проблема, что $x$ не всегда принадлежит $\mathbb{Z}$, поэтому множество целых чисел необходимо расширить. Таким образом вводится множество рациональных чисел $\mathbb{Q}$ с элементами $\frac{p}{q}$, где $p\in \mathbb{Z}$ и $q\in \mathbb{N}$. Множество $\mathbb{Z}$ является подмножеством, в котором каждый элемент $q=1$, следовательно $\mathbb{Z}\subset \mathbb{Q}$ и операции сложения и умножения распространяются и на это множество по следующим правилам, которые сохраняют все вышеперечисленные свойства и на множестве $\mathbb{Q}$:
$\frac{p_1}{q_1}+\frac{p_2}{q_2}=\frac{p_1\cdot q_2+p_2\cdot q_1}{q_1\cdot q_2}$
$\frac{p-1}{q_1}\cdot \frac{p_2}{q_2}=\frac{p_1\cdot p_2}{q_1\cdot q_2}$
Деление вводится таким образом:
$\frac{p_1}{q_1}:\frac{p_2}{q_2}=\frac{p_1}{q_1}\cdot \frac{q_2}{p_2}$
На множестве $\mathbb{Q}$ уравнение $a\cdot x=b$ имеет единственное решение для каждого $a\neq 0$ (деление на ноль не определено). Это значит, что существует обратный элемент
$\frac{1}{a}$ or $a^{-1}$:
$(\forall a\in \mathbb{Q}\setminus\lbrace 0\rbrace)(\exists \frac{1}{a})(a\cdot \frac{1}{a}=\frac{1}{a}\cdot a=a)$
Порядок множества $\mathbb{Q}$ можно расширить таким образом:
$\frac{p_1}{q_1}
Множество $\mathbb{Q}$ имеет одно важное свойство: между любыми двумя рациональными числами находится бесконечно много других рациональных чисел, следовательно, не существует двух соседних рациональных чисел, в отличие от множеств натуральных и целых чисел.
Иррациональные числа $\mathbb{I}$
Примеры иррациональных чисел:
$\sqrt{2} \approx 1.41422135...$
$\pi \approx 3.1415926535...$
Ввиду того, что между любыми двумя рациональными числами находится бесконечно много других рациональных чисел, легко можно сделать ошибочный вывод, что множество рациональных чисел настолько плотное, что нет необходимости в его дальнейшем расширении. Даже Пифагор в свое время сделал такую ошибку. Однако, уже его современники опровергли этот вывод при исследовании решений уравнения $x\cdot x=2$ ($x^2=2$) на множестве рациональных чисел. Для решения такого уравнения необходимо ввести понятие квадратного корня, и тогда решение этого уравнения имеет вид $x=\sqrt{2}$. Уравнение типа $x^2=a$, где $a$ - известное рациональное число, а $x$ - неизвестное, не всегда имеет решение на множестве рациональных чисел, и опять возникает необходимость в расширении множества. Возникает множество иррациональных чисел, и такие числа как $\sqrt{2}$, $\sqrt{3}$, $\pi$... принадлежат этому множеству.
Действительные числа $\mathbb{R}$
Объединением множеств рациональных и иррациональных чисел является множество действительных чисел. Поскольку $\mathbb{Q}\subset \mathbb{R}$, снова логично предположить, что введенные арифметические операции и отношения сохраняют свои свойства на новом множестве. Формальное доказательство этого весьма сложно, поэтому вышеупомянутые свойства арифметических операций и отношения на множестве действительных чисел вводятся как аксиомы. В алгебре такой объект называется полем, поэтому говорят, что множество действительных чисел является упорядоченным полем.
Для того, чтобы определение множества действительных чисел было полным, необходимо ввести дополнительную аксиому, различающую множества $\mathbb{Q}$ и $\mathbb{R}$. Предположим, что $S$ - непустое подмножество множества действительных чисел. Элемент $b\in \mathbb{R}$ называется верхней границей множества $S$, если $\forall x\in S$ справедливо $x\leq b$. Тогда говорят, что множество $S$ ограничено сверху. Наименьшая верхняя граница множества $S$ называется супремум и обозначается $\sup S$. Аналогично вводятся понятия нижней границы, множества, ограниченного снизу, и инфинума $\inf S$ . Теперь недостающая аксиома формулируется следующим образом:
Любое непустое и ограниченное сверху подмножество множества действительных чисел имеет супремум.
Также можно доказать, что поле действительных чисел, определенное вышеуказанным образом, является единственным.
Комплексные числа$\mathbb{C}$
Примеры комплексных чисел:
$(1, 2), (4, 5), (-9, 7), (-3, -20), (5, 19),...$
$1 + 5i, 2 - 4i, -7 + 6i...$ где $i = \sqrt{-1}$ или $i^2 = -1$
Множество комплексных чисел представляет собой все упорядоченные пары действительных чисел, то есть $\mathbb{C}=\mathbb{R}^2=\mathbb{R}\times \mathbb{R}$, на котором операции сложения и умножения определены следующим образом:
$(a,b)+(c,d)=(a+b,c+d)$
$(a,b)\cdot (c,d)=(ac-bd,ad+bc)$
Существует несколько форм записи комплексных чисел, из которых самая распространенная имеет вид $z=a+ib$, где $(a,b)$ - пара действительных чисел, а число $i=(0,1)$ называется мнимой единицей.
Легко показать, что $i^2=-1$. Расширение множества $\mathbb{R}$ на множество $\mathbb{C}$ позволяет определить квадратный корень из отрицательных чисел, что и послужило причиной введения множества комплексных чисел. Также легко показать, что подмножество множества $\mathbb{C}$, заданное как $\mathbb{C}_0=\lbrace (a,0)|a\in \mathbb{R}\rbrace$, удовлетворяет всем аксиомам для действительных чисел, следовательно $\mathbb{C}_0=\mathbb{R}$, или $R\subset\mathbb{C}$.
Алгебраическая структура множества $\mathbb{C}$ относительно операций сложения и умножения имеет следующие свойства:
1. коммутативность сложения и умножения
2. ассоциативность сложения и умножения
3. $0+i0$ - нейтральный элемент для сложения
4. $1+i0$ - нейтральный элемент для умножения
5. умножение дистрибутивно по отношению к сложению
6. существует единственный обратный элемент как для сложения, так и для умножения.
Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения
является функция
где c - произвольная константа.
- 1. Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e - нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
- 2. Число e является вычислимым (а значит, и арифметическим) числом.
Формула Эйлера, в частности
5. т. н. "интеграл Пуассона" или "интеграл Гаусса"


8. Представление Каталана:

9. Представление через произведение:

10. Через числа Белла:

11. Мера иррациональности числа e равна 2 (что есть наименьшее возможное значение для иррациональных чисел).
Доказательство иррациональности
Предположим, что
где a и b - натуральные числа. Учитывая данное равенство и рассматривая разложение в ряд:

получаем следующее равенство:

Представим данную сумму в виде суммы двух слагаемых, одно из которых - сумма членов ряда по n от 0 до a , а второе - сумма всех остальных членов ряда:

Теперь перенесем первую сумму в левую часть равенства:

Умножим обе части полученного равенства на. Получим
Теперь упростим полученное выражение:
Рассмотрим левую часть полученного равенства. Очевидно, что число целое. Целым является также и число, поскольку (отсюда следует, что все числа вида целые). Тем самым левая часть полученного равенства - целое число.
Перейдем теперь к правой части. Эта сумма имеет вид

По признаку Лейбница этот ряд сходится, и его сумма S есть вещественным числом, заключенное между первым слагаемым и суммой первых двух слагаемых (со знаками), т.е.
Оба эти числа при лежат между 0 и 1. Следовательно, т.е. - правая часть равенства - не может быть целым числом. Получили противоречие: целое число не может быть равно числу, которое не является целым. Это противоречие доказывает, что число e не является рациональным, а следовательно является иррациональным.